Gartner:阿里云蝉联全球第三、亚太第一
本文共 622 字,大约阅读时间需要 2 分钟。
4月23日消息,国际研究机构Gartner发布最新云计算市场追踪数据,阿里云亚太市场排名第一,全球市场排名第三。阿里云亚太市场份额从26%上涨至28%,接近亚马逊和微软总和;全球市场份额从7.7%上涨至9.1%,进一步拉开与第四名谷歌差距,挤压亚马逊份额。
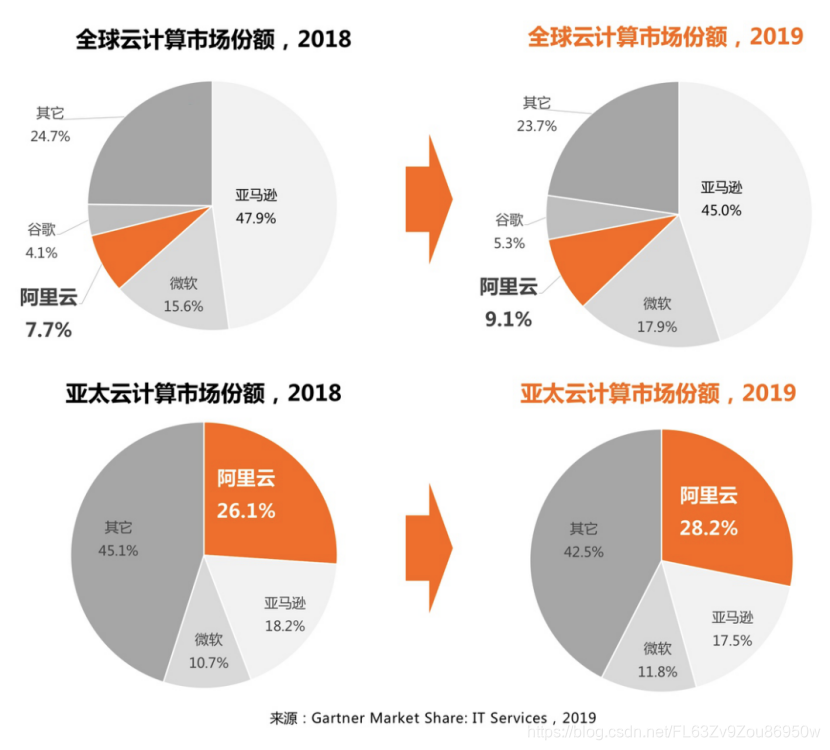
数据显示,2019年全球云计算IaaS市场持续快速增长,同比增长37.3%,总体市场规模达445亿美元。全球市场3A格局稳固,但亚马逊市场份额被微软和阿里云挤压,从2018年48%下降到45%。阿里云排名第三,市场份额增速最快,从2018年的7.7%,上涨至9.1%。
相比全球,亚太市场增长更快,云计算市场规模同比增长达50%。在亚太市场上,阿里云排名第一,市场份额进一步上涨,从2018年的26%上升至28.2%,接近亚马逊和微软总和。同期,亚马逊份额从去年18%下降至17%。
近日,阿里云宣布未来3年投入2000亿,用于云操作系统、服务器、芯片、网络等重大核心技术研发攻坚和面向未来的数据中心建设。3年再投2000亿意味着阿里云的数据中心和服务器规模再翻3倍,冲刺全球最大的云基础设施。
金融时报评论认为,阿里云近年来在中国市场份额不断稳固,2019年第四季度中国市场占比达46%。新冠疫情刺激了市场对远程工作背后的云基础设施与技术的需求,疫情之后,企业和机构将大幅加快上云脚步。
分析师普遍认为,阿里云进一步扩大云基础设施和核心技术投入,“未来数年内赶上亚马逊是大概率事件”。
转载地址:http://cbxe.baihongyu.com/
你可能感兴趣的文章
ONI文件生成与读取
查看>>
Vue 项目中实现高效的消息提示与确认对话框功能(模版)
查看>>
Online PDF to PNG、JPEG、WEBP、 TXT - toolfk
查看>>
onlstm时间复杂度_CRF和LSTM 模型在序列标注上的优劣?
查看>>
onlyoffice新版5.1.2版解决中文汉字输入重复等问题
查看>>
onnx导出动态输入
查看>>
onnx导出动态输入
查看>>
onScrollStateChanged无效
查看>>
onTouchEvent构造器
查看>>
on_member_join 和删除不起作用.如何让它发挥作用?
查看>>
oobbs开发手记
查看>>
OOM怎么办,教你生成dump文件以及查看(IT枫斗者)
查看>>
OOP
查看>>
OOP之单例模式
查看>>
OOP向AOP思想的延伸
查看>>
Vue element 动态添加表单验证
查看>>
OO第一次blog
查看>>
OO第四单元总结
查看>>
OO第四次博客作业
查看>>
OO面向对象编程:第三单元总结
查看>>